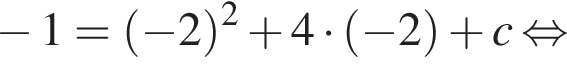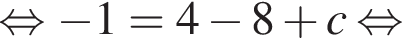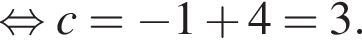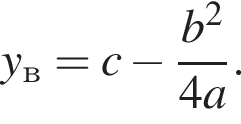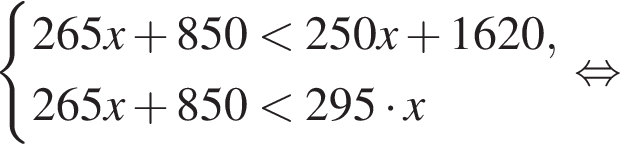Объем конуса равен 9, а его высота равна ![]() Найдите площадь основания конуса.
Найдите площадь основания конуса.
Результат разложения многочлена x (4a − b) + b − 4a на множители имеет вид:
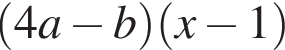
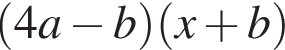
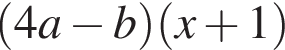
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
На рисунке изображена правильная четырехугольная пирамида. Среди отрезков SB, MQ, SM, SO, MN укажите отрезок, который является апофемой правильной четырехугольной пирамиды.
Из точки A к окружности проведены касательные AB и AC и секущая AM, проходящая через центр окружности O. Точки B, С, M лежат на окружности (см. рис.). Известно, что BK = 4, AC = 9. Найдите длину отрезка AK.
Расположите числа 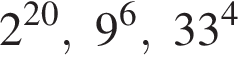 в порядке возрастания.
в порядке возрастания.
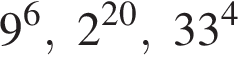
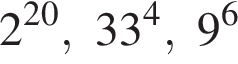
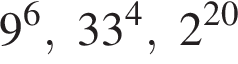
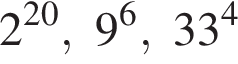
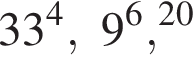
Основание остроугольного равнобедренного треугольника равно 10, а синус противоположного основанию угла равен 0,6. Найдите площадь треугольника.
Если 18% некоторого числа равны 27, то 30% этого числа равны:
В треугольнике ABC известно, что 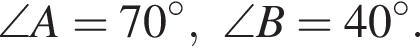 Укажите номер верного утверждения для сторон треугольника.
Укажите номер верного утверждения для сторон треугольника.
На изготовление 25 письменных столов расходуется 3,4 м3 древесины. Сколько кубических метров древесины потребуется на изготовление 110 таких столов?
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 238°. Найдите градусную меру меньшего угла.
Найдите модуль разности наибольшего и наименьшего корней уравнения 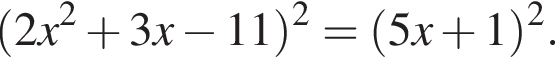
Четырехугольник MNPK, в котором ∠N=136°, вписан в окружность. Найдите градусную меру угла K.
Сумма всех натуральных решений неравенства 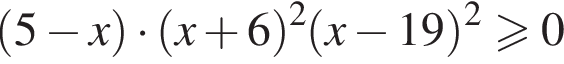 равна:
равна:
Найдите произведение наименьшего решения на количество решений уравнения 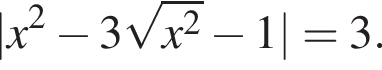
Найдите сумму всех целых чисел из области определения функции 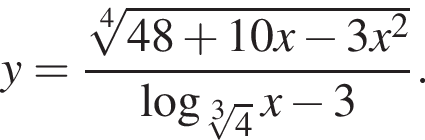
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно точки O.
Известно, что при a, равном −2 и 4, значение выражения 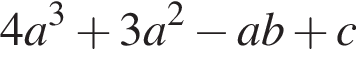 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Решите уравнение 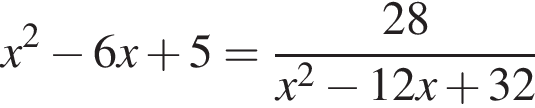 и найдите сумму его корней.
и найдите сумму его корней.
Пусть (x; y) — решение системы уравнений 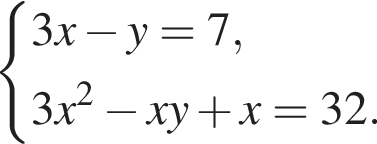
Найдите значение 3y − x.
Решением системы неравенств 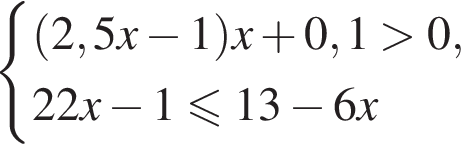 является:
является:
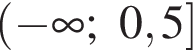
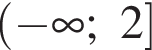


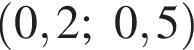
Количество целых решений неравенства 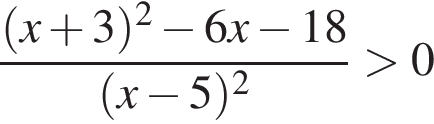 на промежутке
на промежутке 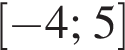 равно:
равно:
Результат упрощения выражения 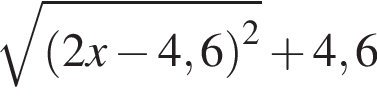 при −1 < x < 1 имеет вид:
при −1 < x < 1 имеет вид:
Пусть x1 и x2 — корни уравнения 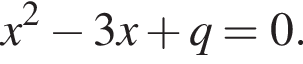 Найдите число q, при котором выполняется равенство
Найдите число q, при котором выполняется равенство 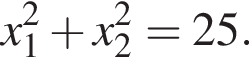
Сумма корней (корень, если он единственный) уравнения 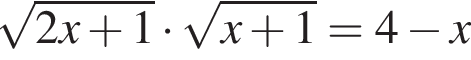 равна (равен):
равна (равен):
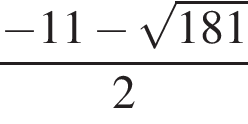
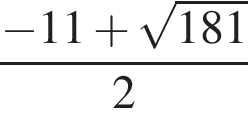
Упростите выражение 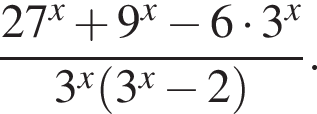
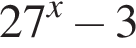
Если ![]() и
и ![]() — корни уравнения
— корни уравнения 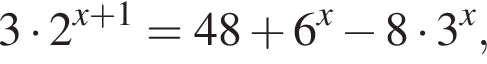 то значение
то значение ![]() равно ... .
равно ... .
Функция y = f(x) определена на множестве действительных чисел ![]() является нечетной, периодической с периодом T = 10 и при
является нечетной, периодической с периодом T = 10 и при  задается формулой
задается формулой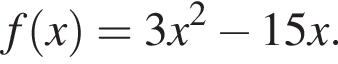 Найдите произведение абсцисс точек пересечения прямой y = 12 и графика функции y = f(x) на промежутке [ −13; 7].
Найдите произведение абсцисс точек пересечения прямой y = 12 и графика функции y = f(x) на промежутке [ −13; 7].
Пусть 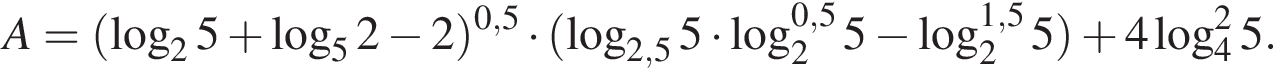
Найдите значение выражения 2A.
Корень уравнения
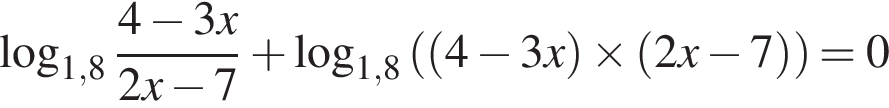
(или сумма корней, если их несколько) принадлежит промежутку:
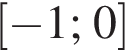
Найдите сумму всех целых решений неравенства 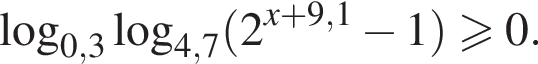
Значение выражения  равно:
равно:
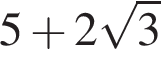
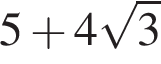
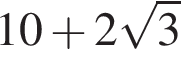
Найдите значение выражения: 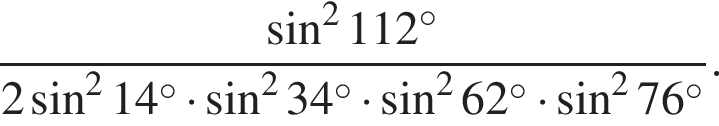
Найдите (в градусах) наибольший отрицательный корень уравнения 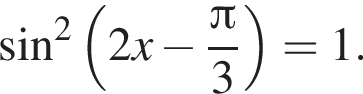
Найдите увеличенную в 25 раз сумму квадратов корней уравнения
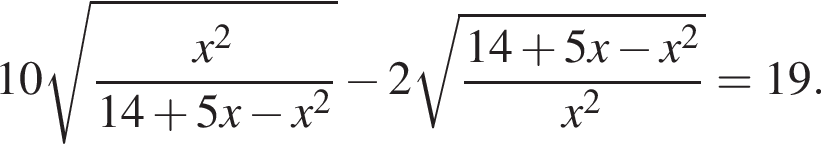
Количество целых решений неравенства 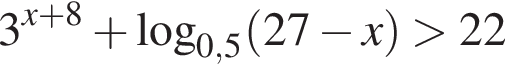 равно ...
равно ...
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 18, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 48, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 18, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 48, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
У Юры есть некоторое количество марок, а у Яна марок в 2 раза больше, чем у Юры. Мальчики поместили все свои марки в один альбом. Среди чисел 26; 38; 20; 37; 39 выберите то, которое может выражать количество марок, оказавшихся в альбоме.
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 5x + 3 = 0. Найдите площадь треугольника.
Функция 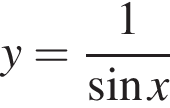 не определена в точке:
не определена в точке:
Используя схематичное изображение параболы
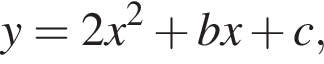 найдите сумму b + c.
найдите сумму b + c.
На диаграмме показано количество посещений сайта на протяжении недели (со вторника по воскресенье). Установите соответствие между вопросами А−В и ответами 1−6.
| Вопрос | Ответ |
|---|---|
A) В какой день недели было на 60 посещений больше, чем в предыдущий? Б) В какой день недели количество посещений было на 20% меньше, чем в среду? B) В какой день недели количество посещений было на 10% больше, чем в предыдущий? | 1) Вторник. 2) Среда. 3) Четверг. 4) Пятница. 5) Суббота. 6) Воскресенье. |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между E и С равно ![]() то ближе других к точке с координатой 1,01 расположена точка:
то ближе других к точке с координатой 1,01 расположена точка:
Известно, что наименьшее значение функции, заданной формулой y = x2 + 4x + c, равно −1. Тогда значение c равно:
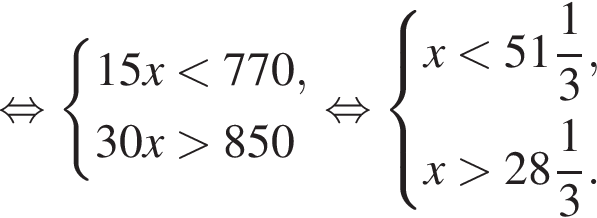
Строительная бригада планирует заказать фундаментные блоки у одного из трех поставщиков. Стоимость блоков и их доставки указана в таблице. При покупке какого количества блоков самыми выгодными будут условия второго поставщика?
| Поставщик | Стоимость фундаментных блоков | Стоимость доставки фундаментных блоков |
|---|---|---|
| 1 | 250 | 1620 |
| 2 | 265 | 850 |
| 3 | 295 | бесплатно |

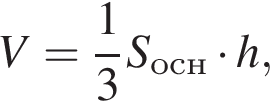 поэтому
поэтому 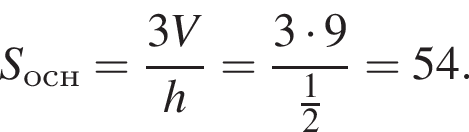

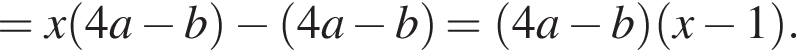

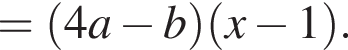
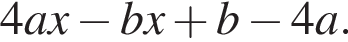
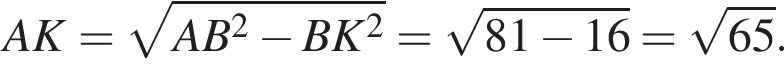
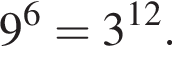 Поскольку все числа положительны, извлечем из каждого корень четвертой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень четвертой степени и получим: 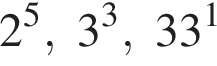 то есть числа 32, 27, 33. Так как 27 < 32 < 33, получаем
то есть числа 32, 27, 33. Так как 27 < 32 < 33, получаем 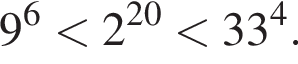
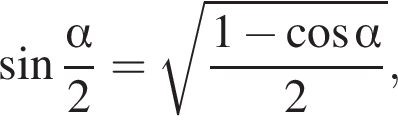 где
где 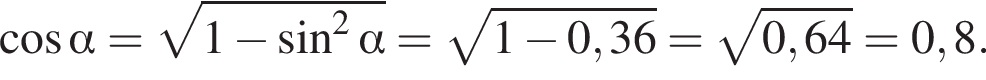
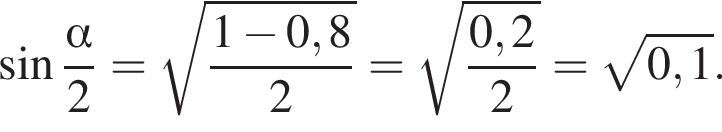
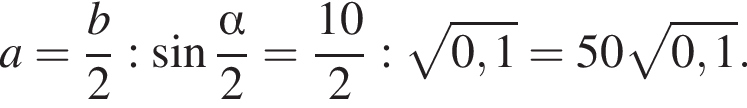 Тогда площадь треугольника равна:
Тогда площадь треугольника равна: 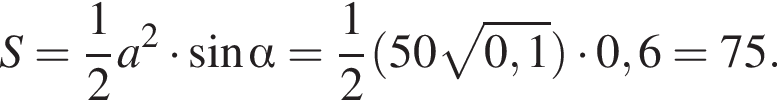
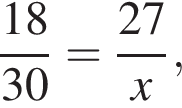 где x — неизвестное число.
где x — неизвестное число.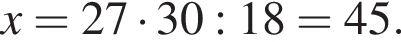
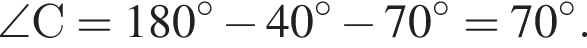 Значит,
Значит, 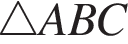 — равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что
— равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что  и
и 
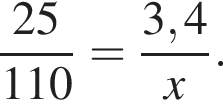 Тогда
Тогда 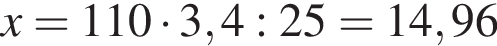 м3.
м3. равна 360°, поэтому четвертый угол равен 122°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 58°.
равна 360°, поэтому четвертый угол равен 122°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 58°.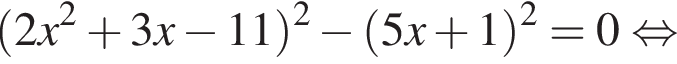
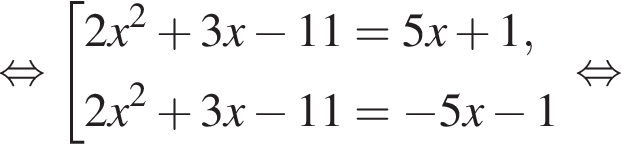
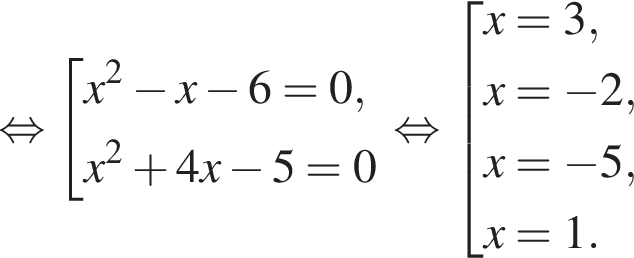
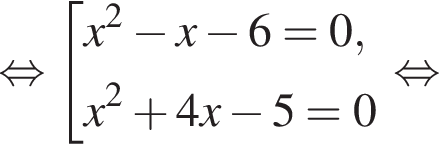
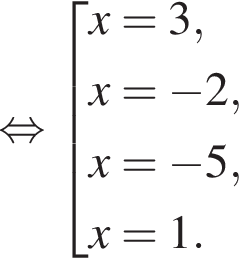
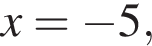 модуль разности наибольшего и наименьшего корней уравнения равен 8.
модуль разности наибольшего и наименьшего корней уравнения равен 8.
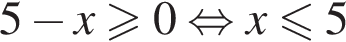 и
и  следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 19. Их сумма равна 34.
следовательно, натуральные решения неравенства: 1, 2, 3, 4, 5, 19. Их сумма равна 34. Имеем:
Имеем: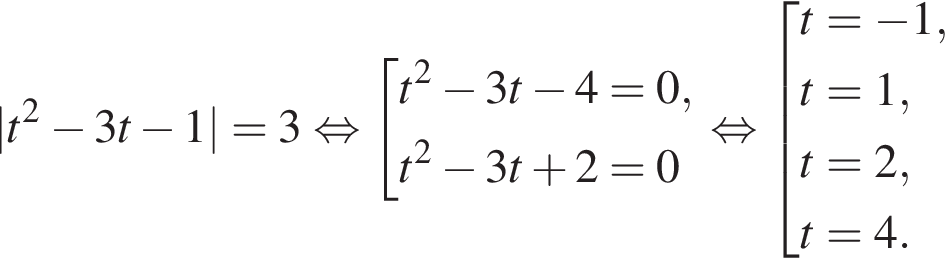
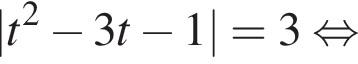
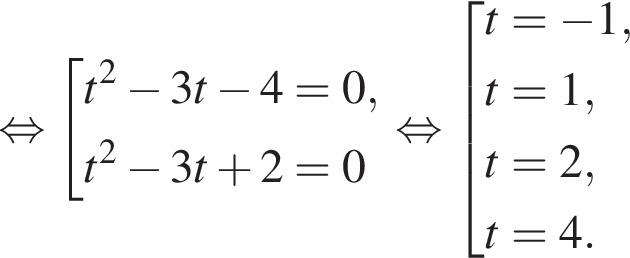
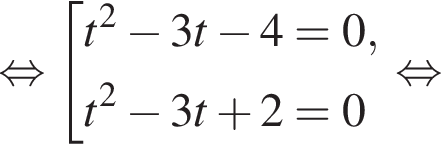
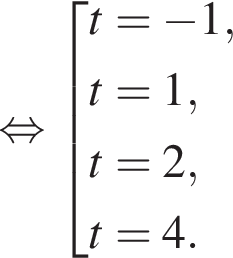
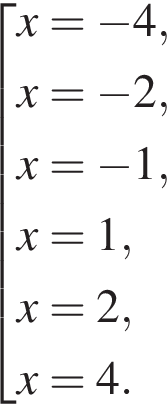

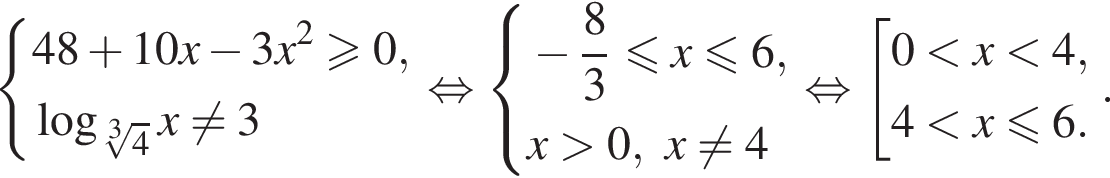
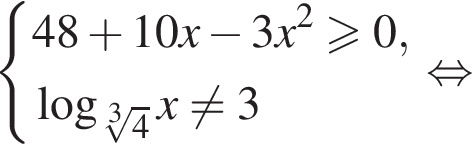
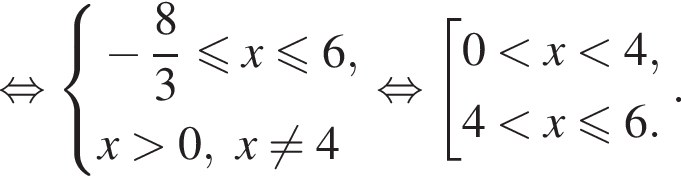
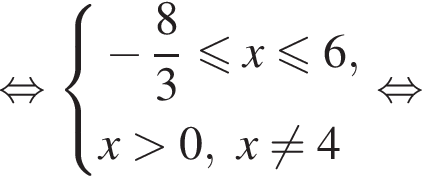
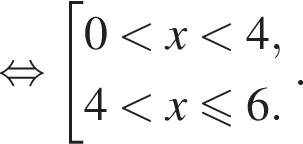
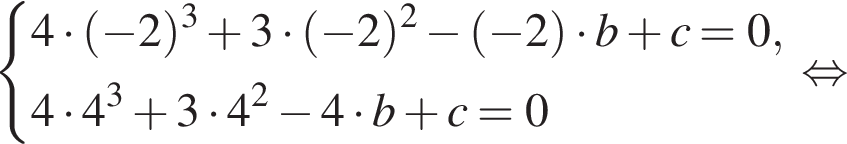
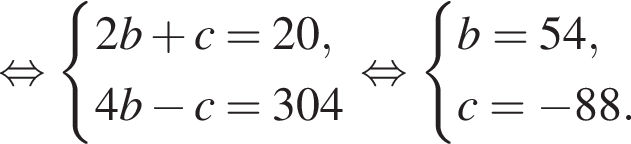
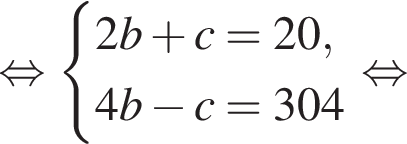
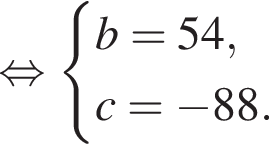

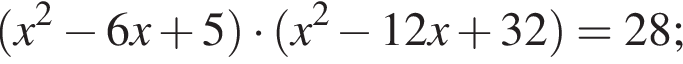


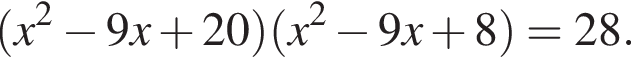
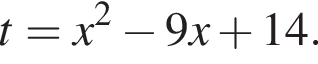 Получим:
Получим: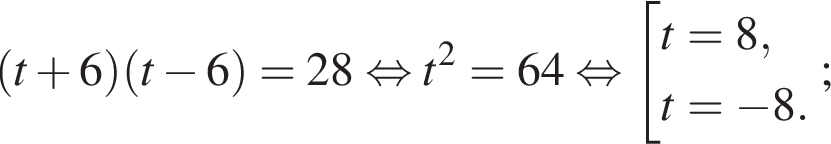
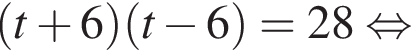
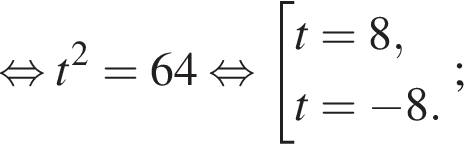
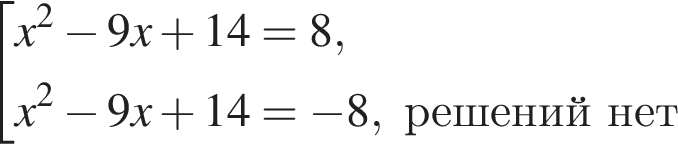
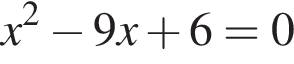 найдем по теореме Виета, она равна 9.
найдем по теореме Виета, она равна 9.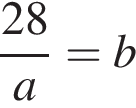 равносильно уравнению
равносильно уравнению  искать ОДЗ не требуется.
искать ОДЗ не требуется.
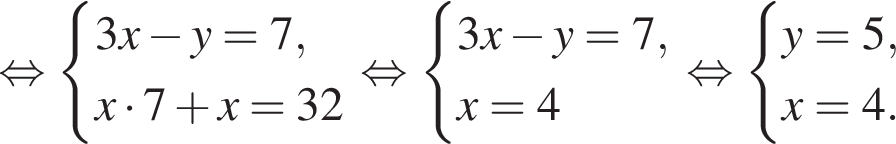
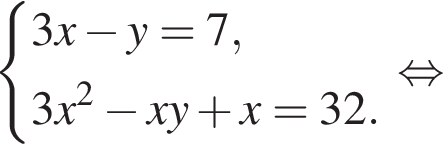
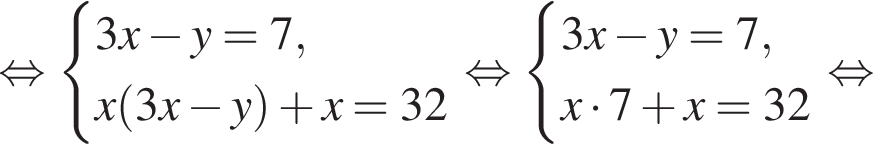
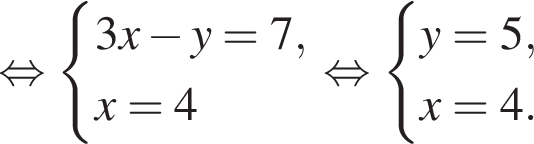
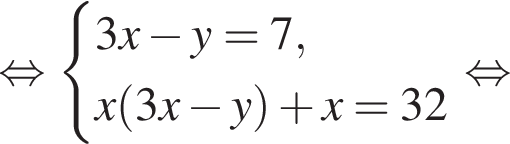
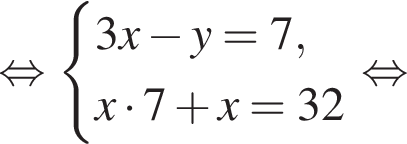
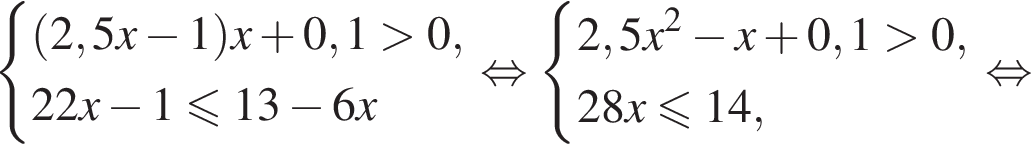
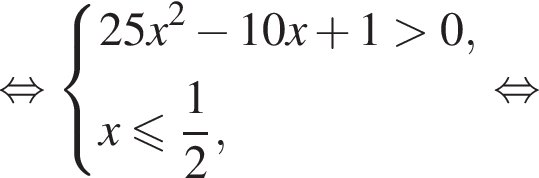
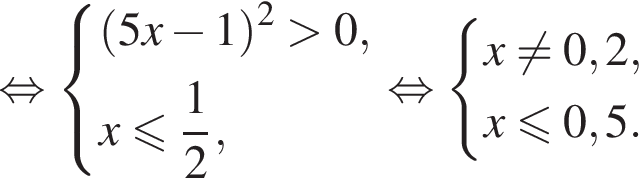
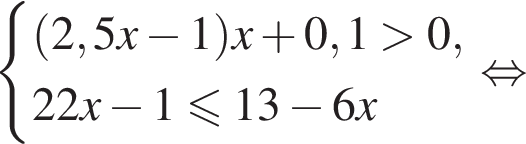
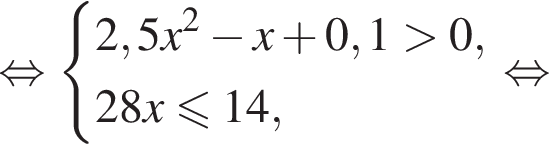
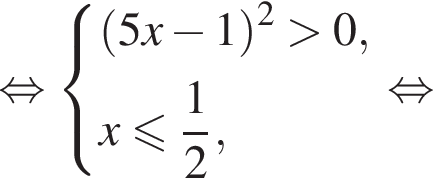
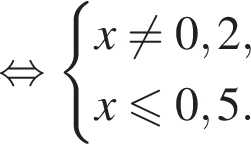
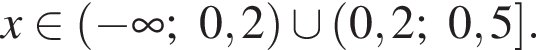
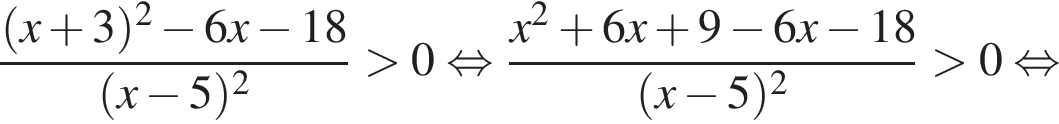
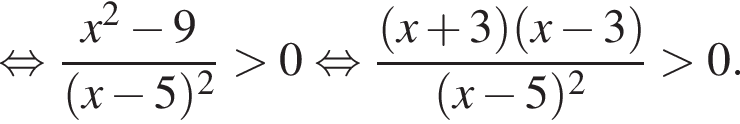
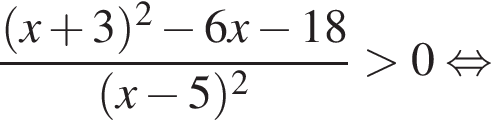
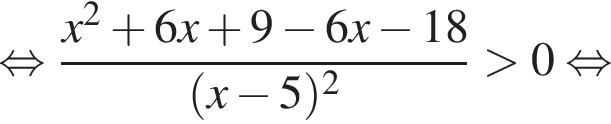
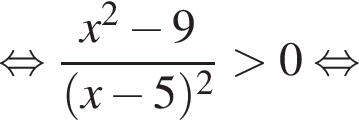
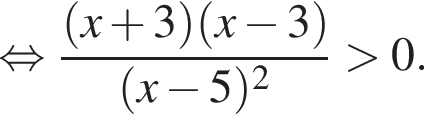
 Корни знаменателя
Корни знаменателя 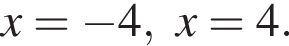 Следовательно, существует только 2 целых решения.
Следовательно, существует только 2 целых решения. 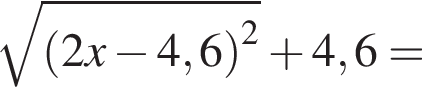
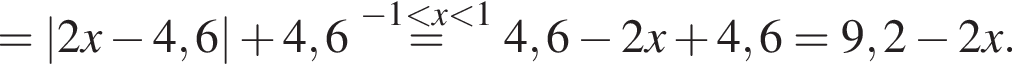
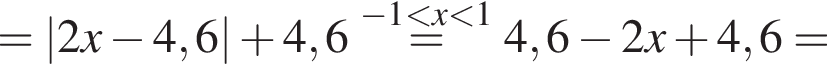
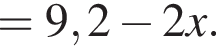
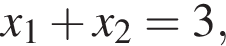 а
а 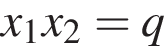
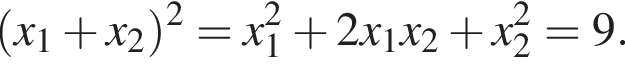 Зная то, что
Зная то, что 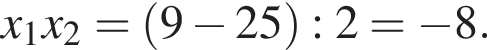
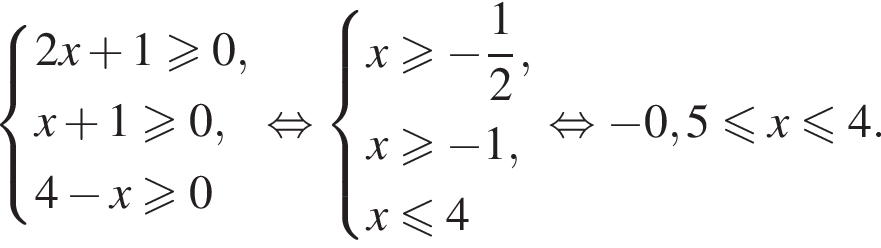
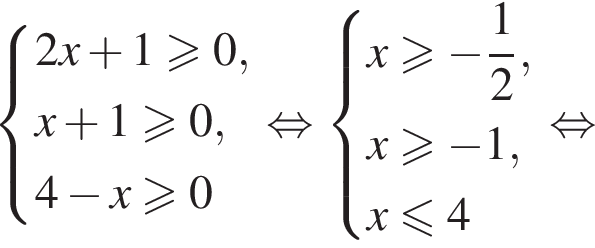
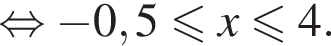
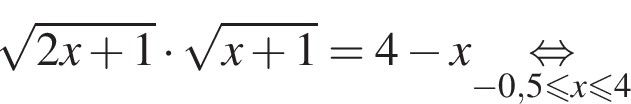
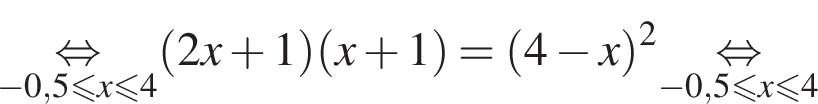
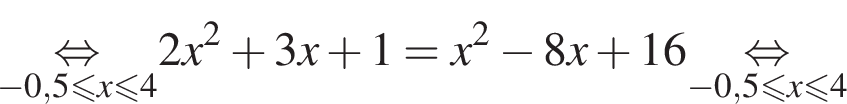
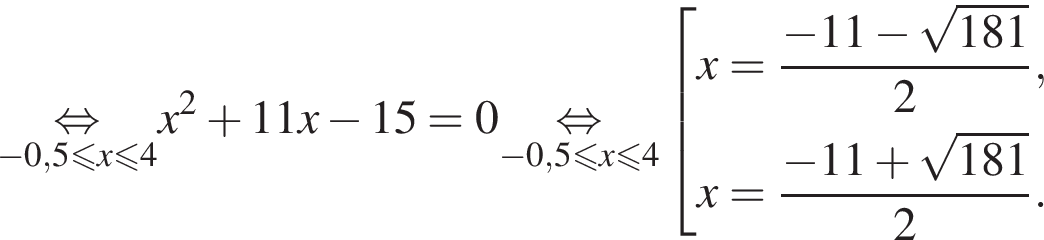
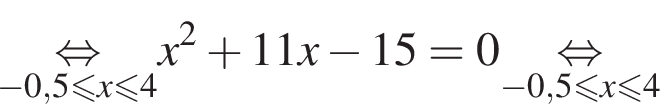
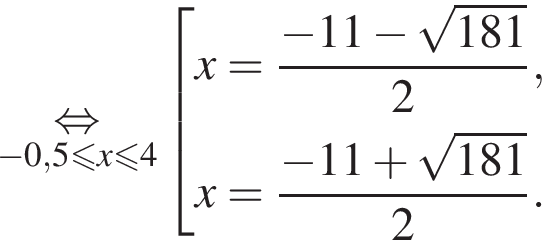
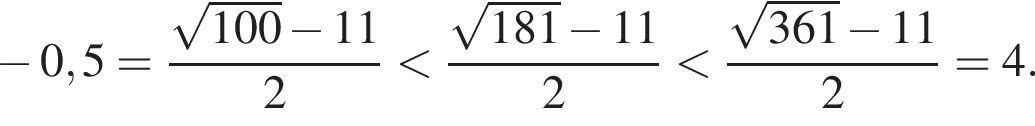
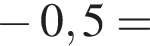
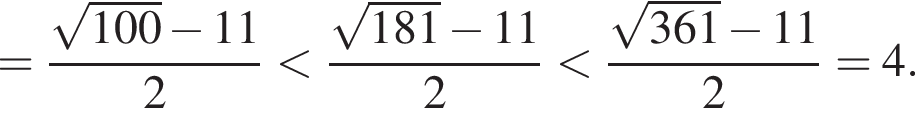
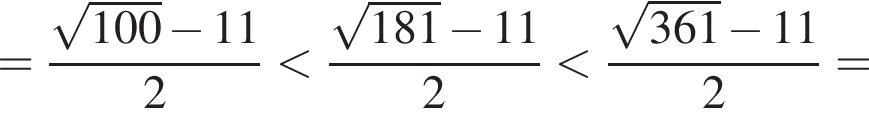
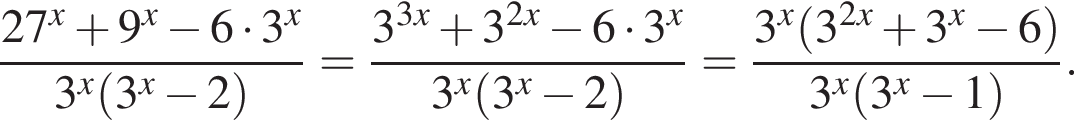
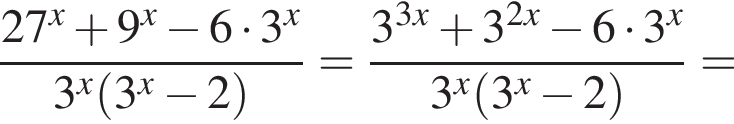
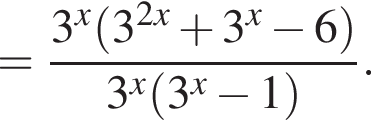
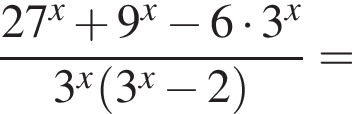
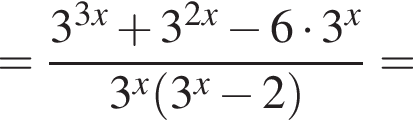
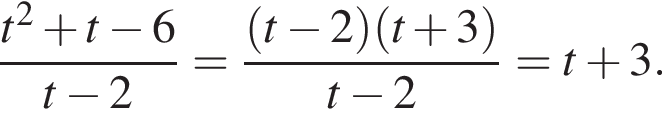 Тем самым, исходное выражение равно
Тем самым, исходное выражение равно 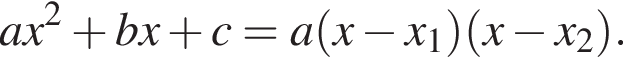
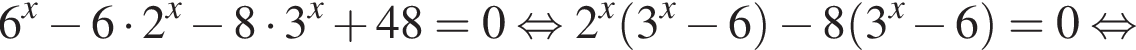
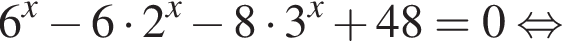
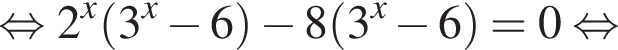
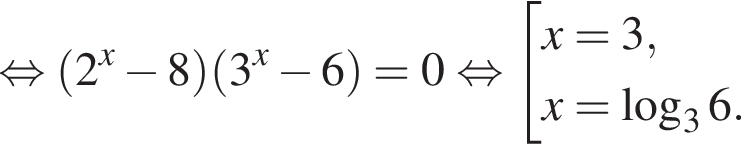
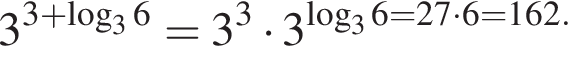
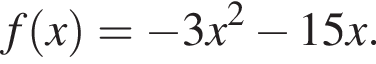 Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 12.
Данный интервал входит в промежуток, на котором необходимо найти произведение абсцисс. Найдем абсциссы точек пересечения полученной функции и прямой y = 12. 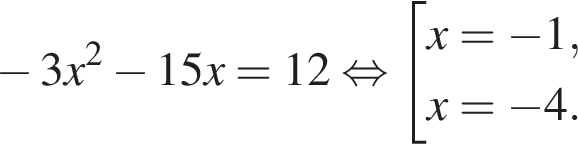
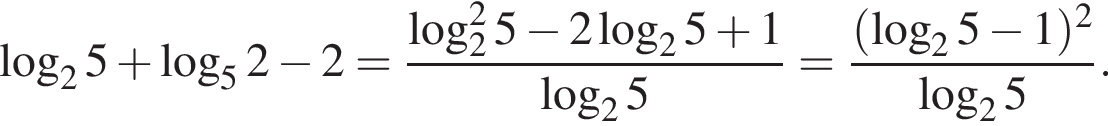
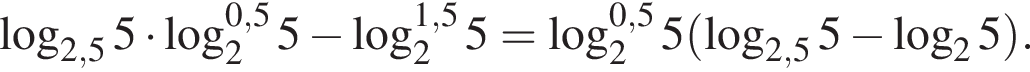
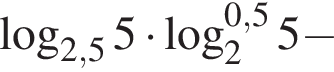
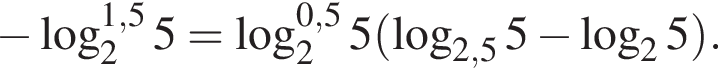
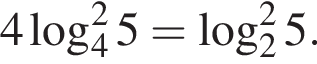 Тогда имеем:
Тогда имеем: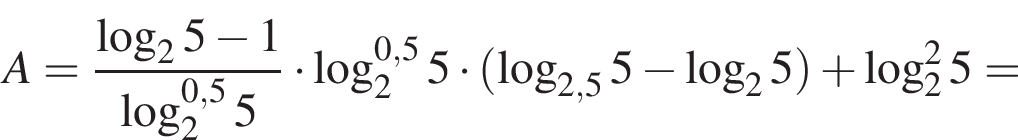
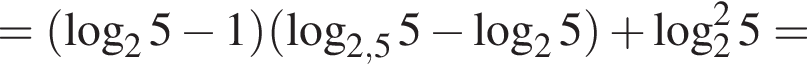
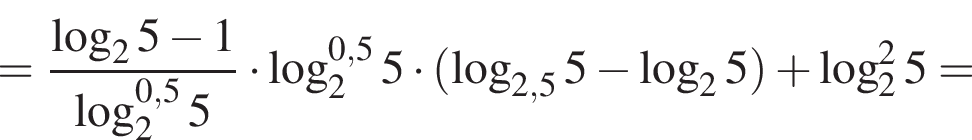
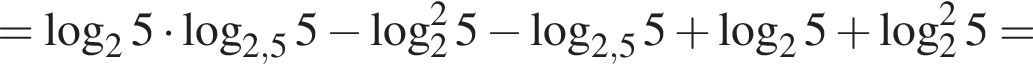
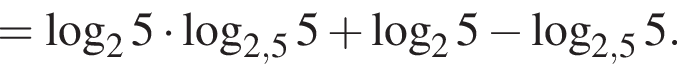
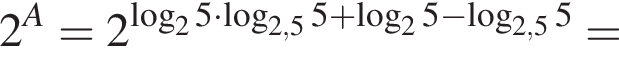
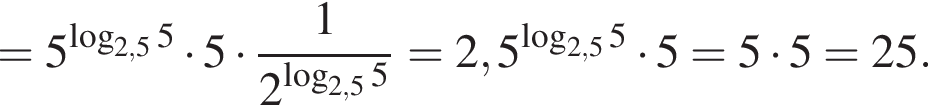
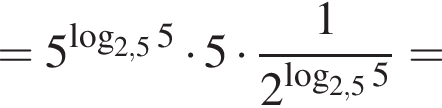
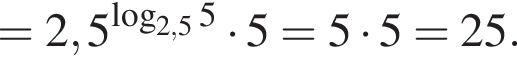
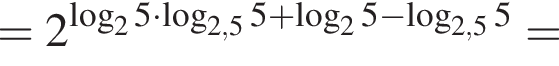
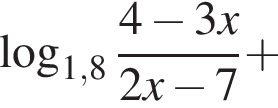
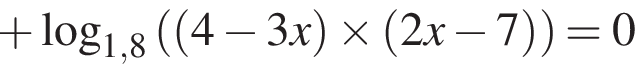
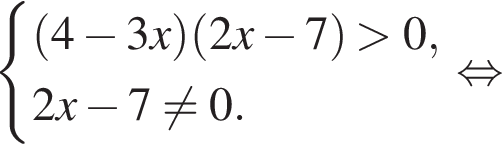
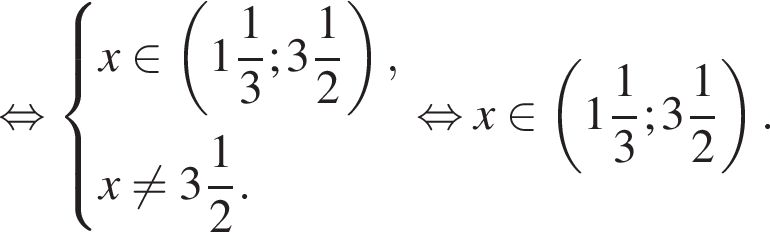
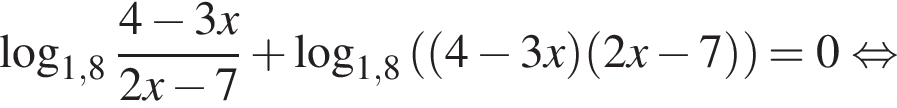
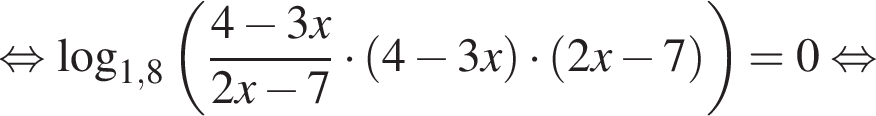
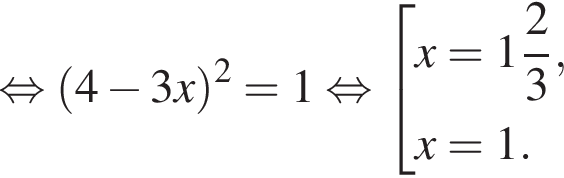
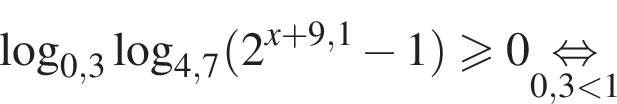
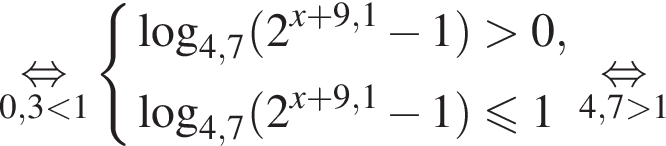
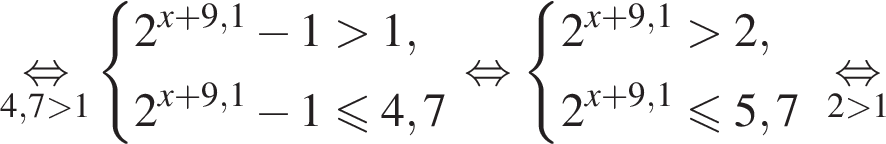
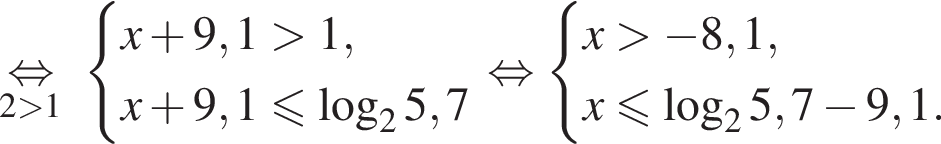
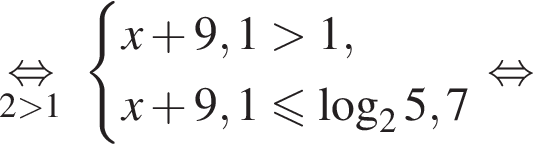
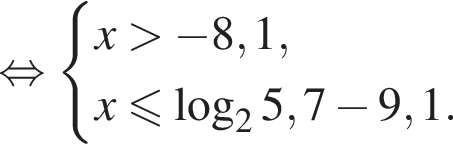
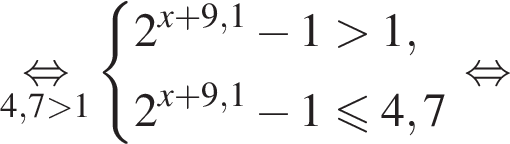
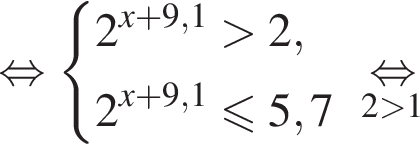
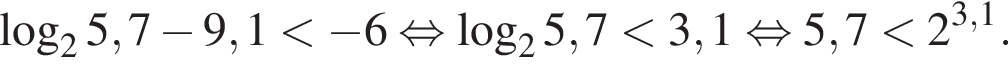
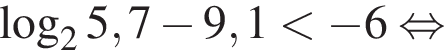
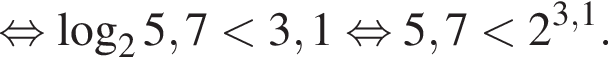
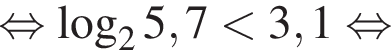

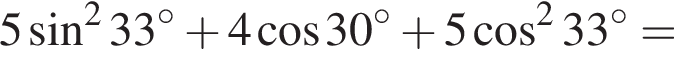
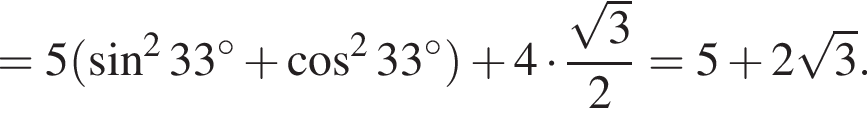
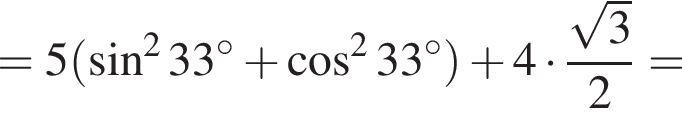
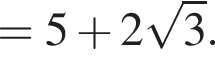

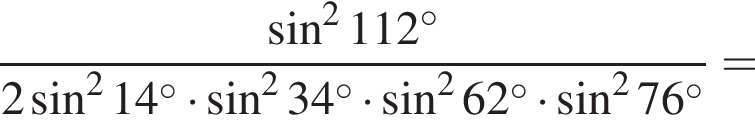
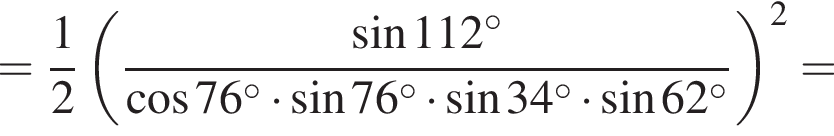
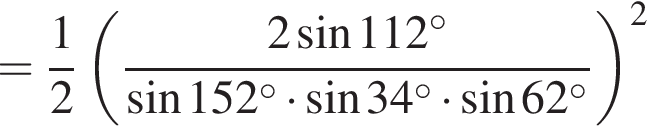
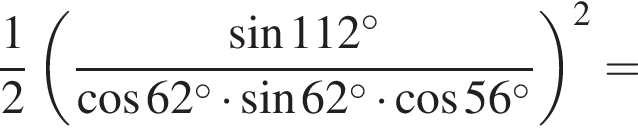
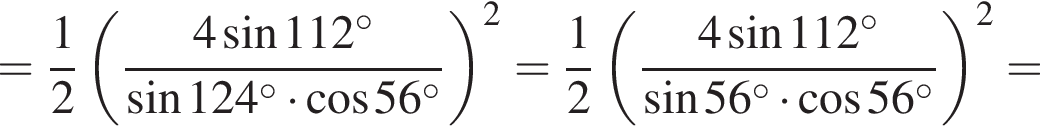
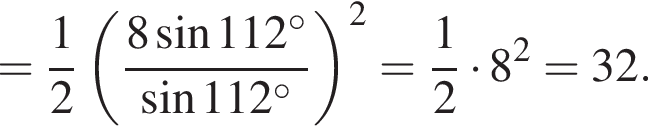
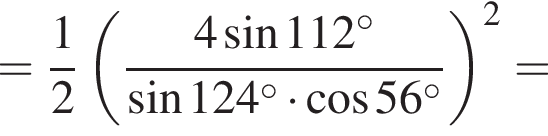
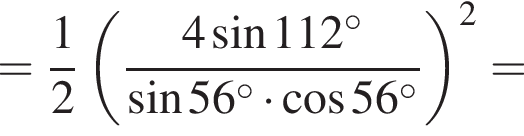
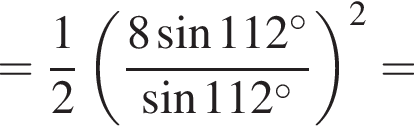
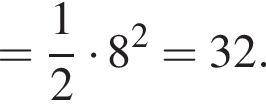
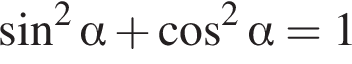 :
: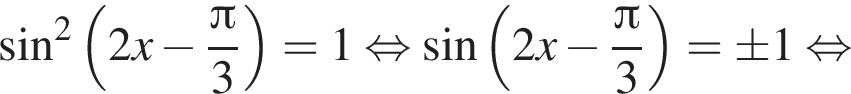
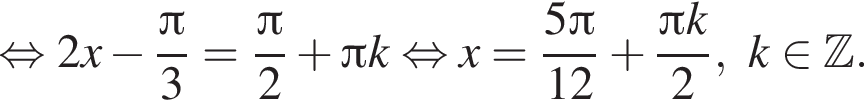
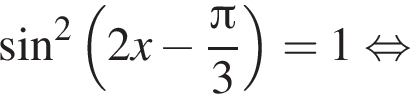
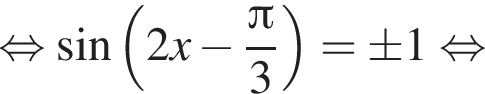
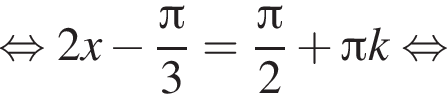
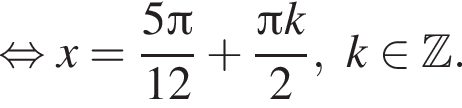
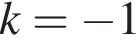 и равен
и равен 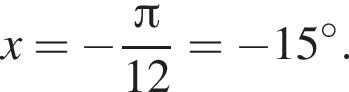
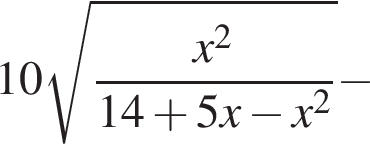
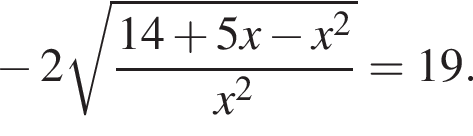
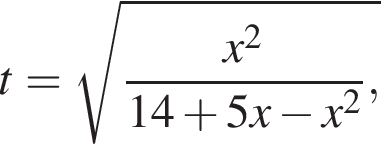
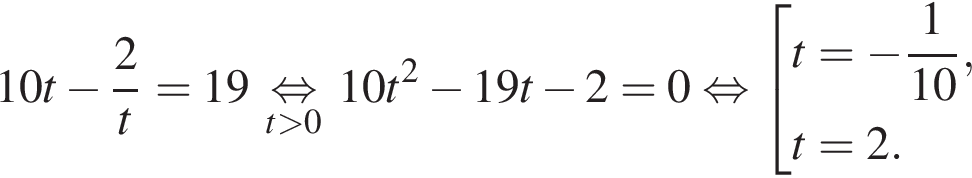
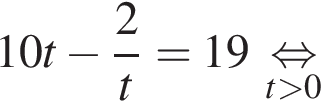
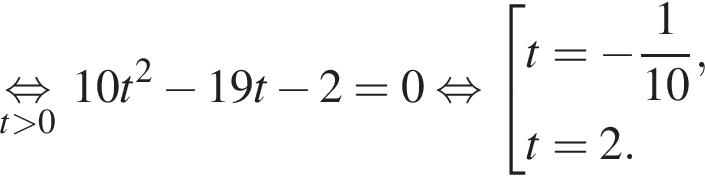
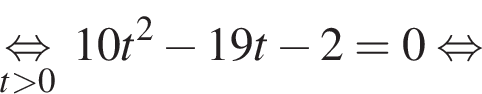
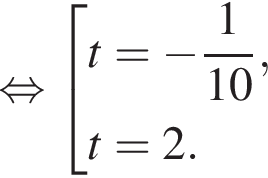
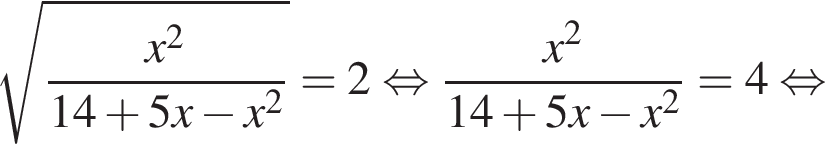
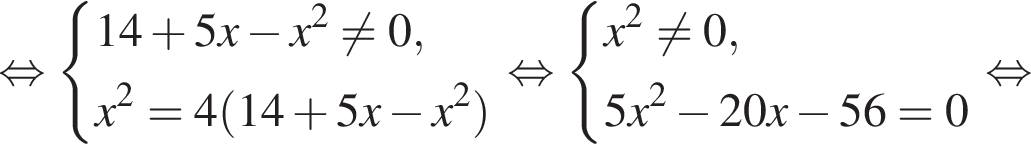
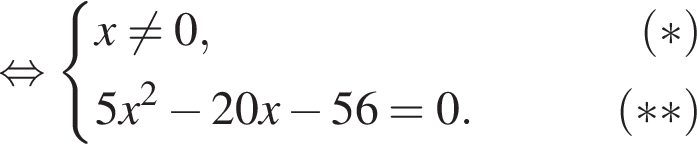
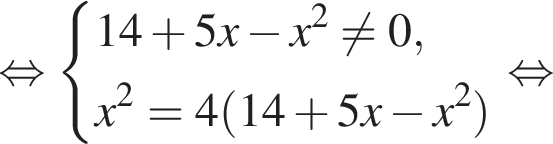
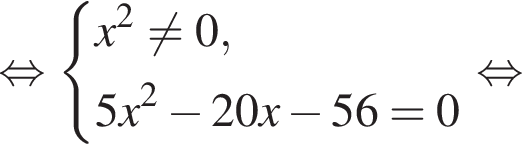
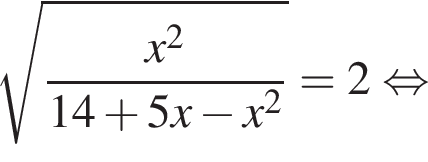
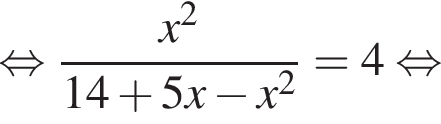
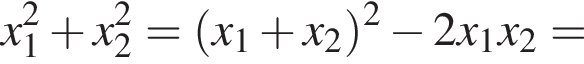
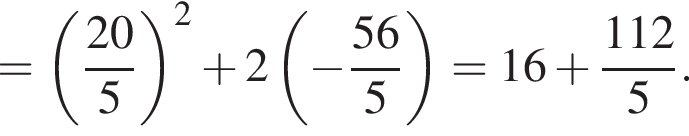
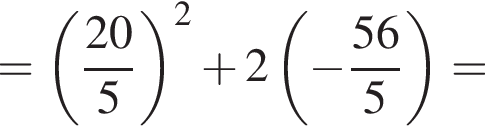
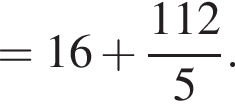
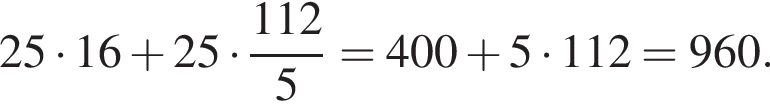
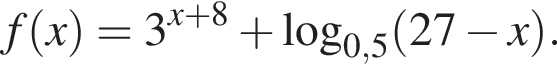 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 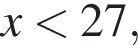 и что на
и что на 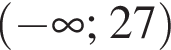
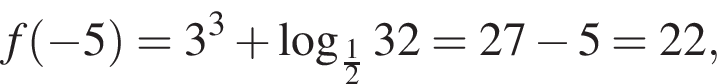 неравенство верно для всех x из
неравенство верно для всех x из 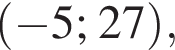 который содержит 31 целое число.
который содержит 31 целое число.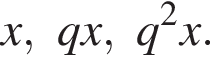
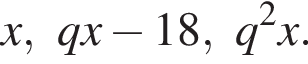
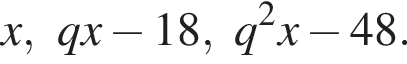
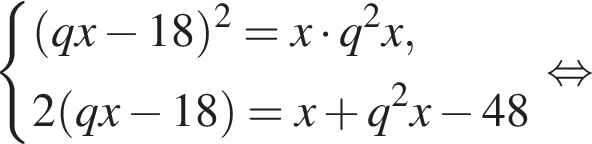
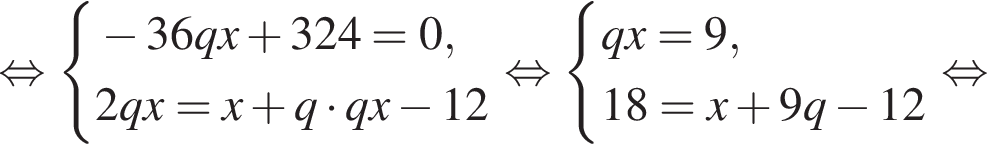
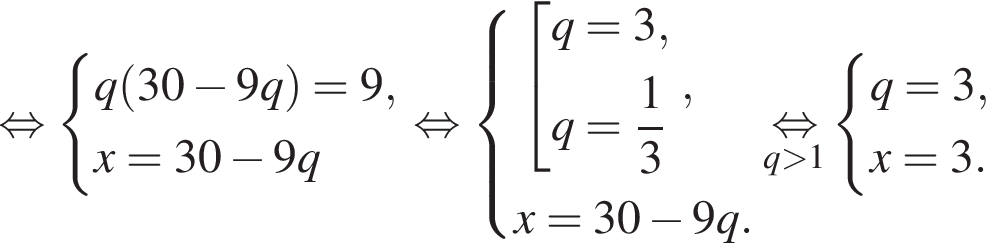
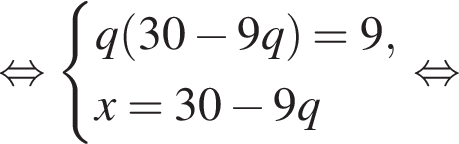
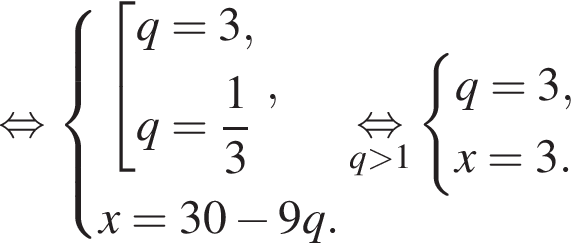
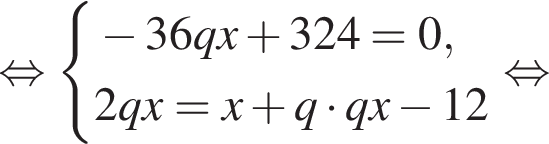
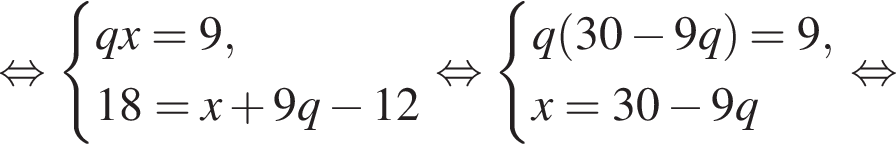
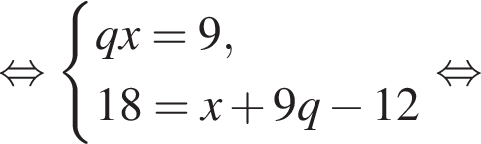
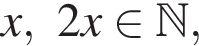 общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.
общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.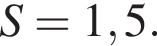
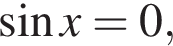 т. е. при
т. е. при 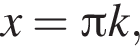 где
где 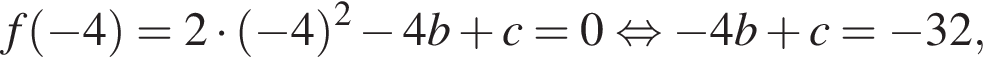
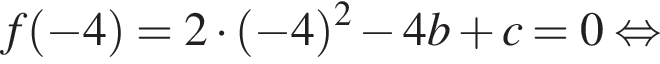
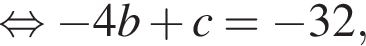
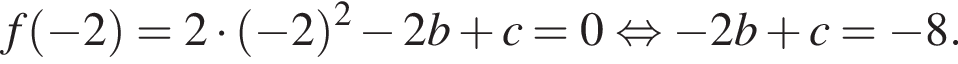
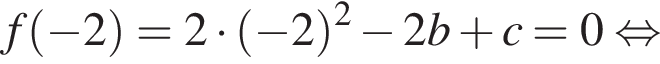

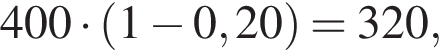 значит, количество посещений на 20% меньше, чем во вторник было в пятницу (4).
значит, количество посещений на 20% меньше, чем во вторник было в пятницу (4).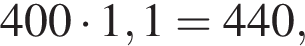 значит, в четверг количество посещений было на 10% больше, чем в предыдущий (3).
значит, в четверг количество посещений было на 10% больше, чем в предыдущий (3).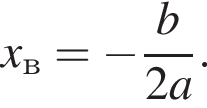 Поэтому
Поэтому 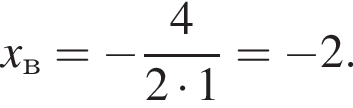 Поскольку y(xв) = −1, имеем:
Поскольку y(xв) = −1, имеем: